Me he encontrado en la wikipedia con esto:
Un número de Fermat es un número natural de la forma:
Pierre de Fermat conjeturó que todos los números naturales de esta forma con n natural eran números primos, pero Leonhard Euler probó que no era así en 1732. En efecto, al tomar n=5 se obtiene un número compuesto:
donde n es natural.
(Esta segunda imagen se ve cortada, al final pone 641 * 6700417)
Aún así me parece un poco precipitada la idea de Fermat, conjeturar algo que se cumple para todos los naturales y que para n = 5 ya no se cumpla, pero vamos, no quiero osar meterme con Fermat. Además Euler hizo el contraejemplo y él tampoco tenía calculadora (que no sé cómo factorizaría el número, supongo que ¿probando hasta la división 641?).
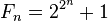

1 comentario:
ese Fermat y sus dichosas conjeturas... hizo sudar tinta a muchos matemáticos durante 358 años con una de ellas escrita en el margen de un libro:
Es imposible descomponer un cubo en dos cubos, un bicuadrado en dos bicuadrados, y en general, una potencia cualquiera, aparte del cuadrado, en dos potencias del mismo exponente. He encontrado una demostración realmente admirable, pero el margen del libro es muy pequeño para ponerla.
Publicar un comentario